Задачи к урокам
Курс 2
Урок 1
1 Задача
Студент за 5 лет учебы сдал 31 экзамен. В каждом следующем году он сдавал больше экзаменов, чем в предыдущем. На пятом курсе экзаменов втрое больше, чем на первом.
Сколько экзаменов на четвертом курсе?
2 Задача
Катя живет на четвертом этаже, а Оля – на втором. Поднимаясь на четвертый этаж, Катя проходит 60 ступенек.
Сколько ступенек надо пройти Оле, чтобы подняться на второй этаж? (первый этаж расположен на уровне земли)
Урок 2
1 Задача
Часовая и минутная стрелки иногда совпадают, например, в 12 или в 24 часа.
Сколько раз они совпадут между 6 часами утра одного дня и 10 часами вечера другого дня?
2 Задача
Для банка заказали новый сейф, имеющий форму прямоугольного параллелепипеда. Высота сейфа 1,5 метра, ширина составляет 9/25 высоты, а глубина 11/18 ширины.
Какое наибольшее количество слитков золота, имеющих форму куба с ребром 9 см, можно положить в этот сейф? (Банк укладывает слитки плотно и ровно друг на друга).
Урок 3
1 Задача
Винни-Пух и Пятачок одновременно отправились в гости друг к другу, но поскольку оба всю дорогу считали пролетавших ворон, то не заметили друг друга при встрече. После встречи Пятачок подошел к дому Винни-Пуха через 4 минуты, а Винни-Пух к дому Пятачка через 1 минуту.
Сколько минут был в пути каждый из них?
2 Задача
Максим, Игорь, Никита и Артем сажали деревья на участках. Максим посадил больше всех – 23 дерева, а Никита меньше всех – 11 деревьев. Сумма количества деревьев, посаженных Игорем и Артемом, делится нацело на 6.
На скольких участках ребята посадили деревья, если на всех участках посадили ровно по 5 деревьев?
Урок 4
На столе выложен треугольник из 6 монет. Требуется за наименьшее количество ходов переложить монеты так, чтобы они образовали кольцо.
Каждый ход состоит в передвигании только одной монеты, другие монеты сдвигать при этом нельзя.
В новом положении каждая монета должна касаться двух других монет. Поднимать монеты с поверхности стола нельзя.
При написании алгоритма используйте команды типа: «1 к (3,6)», где 1 – номер перекладываемой монеты, а 3 и 6 – номера монет, к которым кладется перекладываемая.
Алгоритмов может быть несколько.

Урок 5
Жители Андаманских островов, говорящие на языке беа*, назовут:
первый из двух предметов – otola,
второй из двух – tarolo,
второй из трех – muguchal,
второй из пяти – arolo,
четвертый из пяти – muguchal-tarolo,
пятый из пяти – tarolo,
третий из семи – arolo,
четвертый из семи – muguchal,
первый из девяти – otola,
второй из девяти – arolo,
шестой из девяти – muguchal-tarolo,
седьмой из девяти – muguchal-tarolo.
* Язык беа относится к андаманской семье языков, на нем говорят около 100 человек на острове Южный Андаман.
1 Задача
Как назвать на языке беа первый из пяти предметов, пятый из семи, седьмой из семи, четвертый из девяти, пятый из девяти, восьмой из девяти предметов?
Урок 6
15 спичек выложены в один ряд. Необходимо собрать их в 5 кучек по 3 спички в каждой. Перекладывать спички можно только по одной, каждый раз перескакивая через 3 спички.
При разработке алгоритма решения задачи используйте команды типа: “6 к 10”, где 6 – номер перекладыаемой спички, а 10 – номер спички, к которой кладется перекладываемая. Алгоритмов может быть несколько.
Урок 7
Аборигены архипелага Зокс проживают на пяти островах: Зог, Зоб, Зон, Зоз, Зод. Население всех островов пропорционально их размерам.
Сколько зоксиан проживает на каждом острове и как называются острова в порядке возрастания их размеров, если известно, что:
1. Самый маленький остров населяет 1/10 часть всего народа
2. Самый большой остров – Зод. Самый маленький – не Зоз.
3. На одном острове живет 1/5 часть народа Зокс. На другом острове – 1/3.
4. Зоб – в полтора раза больше, чем один из других островов.
5. На острове Зон на 100 человек больше, чем на самом маленьком.
6. Всего на всех островах проживает 750 аборигенов.
Привести подробное решение.
Урок 8
Бродя по развалинам инопланетного города, космонавты обнаружили обрывок листа, напоминающего нашу бумагу, на котором была записана, видимо маленьким учеником, следующая арифметическая операция:
+ # @
# @
——–
# * #
Известно, что жители этой планеты использовали некую позиционную систему счисления. Помогите космонавтам расшифровать эту запись.
Сколько могло быть пальцев на руках у инопланетян?
Урок 9
1 Задача
а) Переведите число MCMXCVI в десятичную систему счисления.
б) Переведите число 462 в римскую систему счисления.
2 Задача
Двухразрядное число, записанное в четверичной СС при перестановке его цифр равно числу в семеричной СС. Найти оба эти числа или досказать, что такое невозможно.
3 Задача
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30.
Укажите это основание.
Урок 10
1 Задача
В девятеричной системе счисления заданы два числа 3X5 и 5X4, где X – неизвестная цифра. Найдите X, если сумма эти» чисел в десятичной системе равна 783.
2 Задача
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 18 оканчивается на 3.
3 Задача
В саду 100q фруктовых деревьев. Из них: 33q яблони, 22q груши, 16q слив и 17q вишен. Найдите основание системы счисления, в которой посчитаны деревья.
Урок 11
Когда в правильно решенном примере на сложение ОДИНАКОВЫЕ цифры заменили одинаковыми буквами, а РАЗНЫЕ цифры – разными буквами, получилась запись, в которой вместо цифр стоят буквы:
С Л О В О
С Л О В О
С Л О В О
+ С Л О В О
С Л О В О
С Л О В О
С Л О В О
————–
Ф Р А З А
Каким цифрам соответствуют буквы примера? Восстановите пример. Ответ объясните.
Урок 12
Сергеев, Панин, Борисов и Леднев решили посоревноваться на звание лучшего рыбака. Они договорились каждую рыбу оценивать по-разному: за судака рыбак получал 5 очков, за леща – 4, за окуня – 2, а за ерша – 1 очко.
Единственного судака поймал Сергеев. Было выловлено всего 3 окуня. Все рыбаки вместе набрали 18 очков. Меньше всего очков получил Панин, хотя он и наловил больше всех. Панин и Борисов вместе набрали столько же очков, сколько Сергеев и Леднев вместе. И, наконец, у всех оказалось разное количество очков.
Определить, какой улов был у каждого из рыбаков? Ответ объяснить.
Урок 13
Известный программист Петя Торопыжкин составил для себя программу сбора в школу:
Начало: вскочить с постели; надеть рубашку; надеть пиджак; надеть правый ботинок; посмотреть на часы, если вскочил на несколько минут раньше, то лечь подремать; в противном случае надеть брюки; надеть левый носок; сходить умыться; если портфель не собран, то собрать; в противном случае позавтракать; надеть правый носок; надеть галстук и пиджак; надеть левый ботинок; если холодно, то надеть пальто; надеть шапку; выбежать из дома; вернуться назад; взять портфель; выбежать из дома; забежать за Вовкой; если он дома и еще завтракает, то, если есть время, позавтракать вместе с ним и бежать в школу вместе; в противном случае бежать в школу одному; конец.
Цель программы: в любом случае Петя должен прийти в школу нормально одетым, сытым и с портфелем.
Ошибками являются:
1) операторы или группы операторов, которые при каких-либо стечениях обстоятельств или в любом случае не позволяют достигнуть цели.
2) отсутствие операторов, обеспечивающих достижение цели.
Ваша задача: выписать все ошибки и объяснить, почему это ошибки.
Урок 14
Вот таблица одного из чемпионатов по футболу Великобритании:
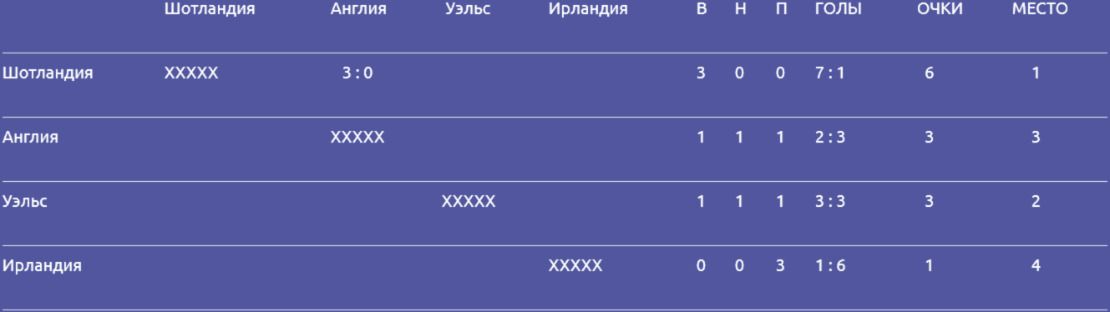
В таблице В – выигрыш; П – проигрыш; Н – ничья.
Очки считаются так: за выигранную игру команда получает 2 очка; за ничью 1 очко за проигранную игру 0 очков.
Урок 15
Восстановить пример:
+ КИТО
КИОТО
_______
ТОКИО
Пример выполнен верно.